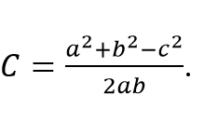მათემატიკის სპეციალისტი: „2025 წლის აბიტურიენტთა საგამოცდო პროგრამაში ამოღებულია 3 საკითხი – სამი მთავარი თემა“

მათემატიკის მეცნიერებათა დოქტორი, თბილისის ალექსანდრე ცინცაძის სახელობის 150-ე საჯარო სკოლის წამყვანი მასწავლებელი მათემატიკაში, მურმან კინწურაშვილი EDU.ARIS.GE-სთან 2025 წლის ერთიანი ეროვნული გამოცდების მათემატიკის პროგრამას აფასებს და ამბობს, რომ სხვა საგნების მსგავსად, ცვლილებები მათემატიკაშიც შევიდა. აღნიშნულის გათვალისწინებით ის სასკოლო სახელმძღვანელოებში მოსალოდნელ საფრთხეზე მიუთითებს და ხაზგასმით ამბობს, რომ აღნიშნული დაუშვებელია.

სპეციალისტის წერილს ჩვენი კითხვის პასუხად უცვლელად წარმოგიდგენთ:

„მოგახსენებთ, რომ მათემატიკის საბაზო საფეხურის სტანდარტი შედგება შემდეგი მიმართულებებისაგან: რიცხვები და მოქმედებები; ალგებრა და კანონზომიერება; გეომეტრია და სივრცის აღქმა (გაზომვა); სტატისტიკა და ალბათობა.

საშუალო საფეხურის სტანდარტი შედგება შემდეგი მიმართულებისაგან: რიცხვები და მოქმედებები; ალგებრა და კანონზომიერება; გეომეტრია და სივრცის აღქმა (გაზომვა); სტატისტიკა და ალბათობა; ლოგიკის საწყისები.

2024 წლის ერთიანი ეროვნული გამოცდებისთვის მათემატიკის საგამოცდო პროგრამა შედგებოდა შემდეგი საკითხებისაგან: ალგებრა მოიცავდა 43 ქვესაკითხს; გეომეტრია (პლანიმეტრია-სტერეომეტრია) პლანიმეტრია მოიცავდა 43 ქვესაკითხს, სტერეომეტრია 23 ქვესაკითხს. მონაცემთა ანალიზი, ალბათობა და სტატისტიკა 3 ქვესაკითხს და ზომის ერთეულები 6 ქვესაკითხს.

ახალ, 2025 წლის საგამოცდო პროგრამაში ამოღებულია 3 საკითხი – სამი მთავარი თემა პლანიმეტრიიდან: სინუსების თეორემა; კოსინუსების თეორემა და სამკუთხედების ამოხსნა.

2025 წლის საგამოცდო პროგრამები ერთიანი ეროვნული გამოცდებისთვის

შედარებისთვის: 

2024 წლის საგამოცდო პროგრამები ერთიანი ეროვნული გამოცდებისთვის

მიუხედავად იმისა, რომ ეს საკითხები არ არის პროგრამაში შეტანილი ეს არ ნიშნავს იმას, რომ მასწავლებელმა არ ასწავლოს მოსწავლეებს ზემოთ აღნიშნული საკითხები, რადგან სინუსებისა და კოსინუსების თეორემები ძირითადი ინსტრუმენტებია სამკუთხედების ამოხსნაში, ტრიგონომეტრიული ამოცანების გადაჭრაში და მათემატიკის პრაქტიკულ გამოყენებებში.

კოსინუსების თეორემა პირდაპირ უკავშირდება ვექტორების სკალარულ ნამრავლს, ვექტორებით სამკუთხედის გადაჭრისას, კოსინუსებისა და სინუსების თეორემები გამოყენებადია როგორც სიგრძეების, ისე კუთხეების გამოთვლისთვის. ისინი გეომეტრიის, ფიზიკის, ალგებრისა და გამოყენებითი მეცნიერებების განუყოფელი ნაწილია, რაც მათ უნივერსალურ მნიშვნელობას აძლევს. კოსინუსების თეორემის გადახარისხებით შეიძლება გამოვთვალოთ კუთხე C;

თუ მოცემულია სამკუთხედის ორი გვერდი და მათ შორის კუთხე, კოსინუსების თეორემა საშუალებას გვაძლევს, გამოვთვალოთ მესამე გვერდი. კოსინუსების თეორემა ხელს უწყობს რთული ტრიგონომეტრიული ამოცანების ამოხსნას, განსაკუთრებით მრავალკუთხედებსა და წრიულ ფიგურებში.

შეჯამების სახით, შეიძლება ითქვას, რომ შესაძლოა, ზოგიერთ გრიფირებულ სახელმძღვანელოში არ იყოს შეტანილი სინუსებისა და კოსინუსების თეორემა, რაც დაუშვებლად მიმაჩნია. იმედს ვიტოვებ, რომ სახელმძღვანელოს ავტორები შეეცდებიან შემდგომი გამოცემისათვის აღმოფხვრან ეს ლაფსუსი და გამართონ სახელმძღვანელოები“.

ამავე თემაზე:

„ვინც ამ პროგრამის შემუშავებაში მონაწილეობდა, ოდნავადაც არა აქვს წარმოდგენა, რა კრიტერიუმებით უნდა შეფასდეს ლიტერატურული ტექსტი“

ქართულის სპეციალისტი საგამოცდო პროგრამაში ცვლილებებზე: „სანამ წიოკს დავიწყებდეთ, რამდენიმე „მარტივი ჭეშმარიტება“ გავიმეოროთ“

„ეროვნული გამოცდების პროგრამების ჩამონათვლიდან როცა ამოიღებ ილიას „ბენდიერ ერს“, განდეგილს“, გასაგებია თუ რა იდეით იმართება „განათლების“ სისტემა“